AI对抗攻击：FGSM (快速梯度符号方法)

FGSM简介

FGSM(Fast Gradient Sign Method ) 是一种简单容易实现的对抗攻击方法，最早由Ian J. Goodfellow, Jonathon Shlens, 和 Christian Szegedy 提出。

其效果可见下图¹：

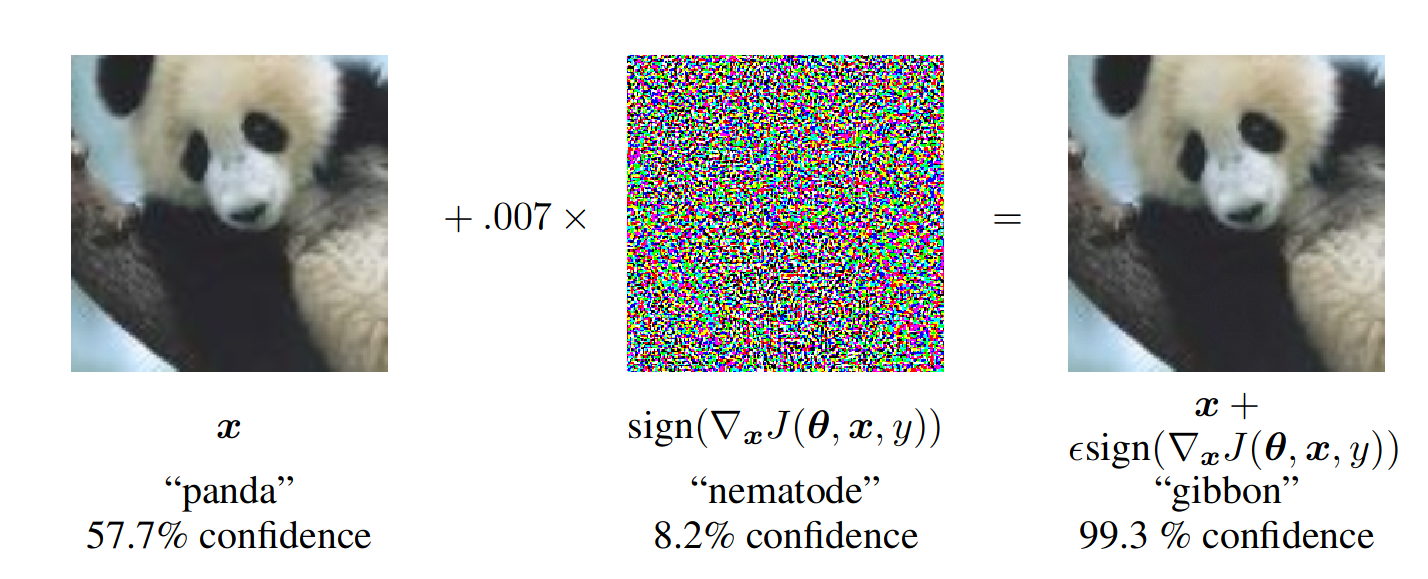
如上图，FGSM的实现公式可表示为：

$$ x^{\prime}=x+\epsilon\cdot\mathrm{sign}(\nabla_{x}J(\theta,x,y)) $$

其中$J(\theta,x,y)$ 为损失函数，$x$为输入的图像，$y$为真实的标签，

iFGSM简介

iFGSM中的i，意为ilterate，即迭代。意思就是反复多次使用FGSM，以此达到更好的效果。用公式可以表示为：

$$ x^{(0)}=x \\x^{(i+1)}=\mathrm{Clip}_{x,\epsilon}\left(x^{(i)}+\epsilon\cdot\mathrm{sign}(\nabla_{x}J(\theta,x^{(i)},y))\right) $$

FGSM与iFGSM效果比较

从下图可以看出，在添加的噪声赋值近似的条件下（$\epsilon_{\mathrm{FGSM}} = i*\epsilon_{\mathrm{iFGSM}}$），iFGSM可以拥有更好的效果。

FGSM($\epsilon=0.01$)	iFGSM（$\epsilon=0.001,i=10$）

从无攻击到针对性攻击

上面的示例均为非针对性攻击，它可以让网络输出错误的结果，但是无法控制结果是什么；而针对性攻击，不仅可以让网络输出错误的结果，还可以控制输出的结果。

Target is wrench	Targeted is dragonfly

对于无目标FGSM，我们的想法是：

$$ \operatorname{maxmize}J(\theta,x^{\prime},y), \quad \text{s.t.}\|x^{\prime}-x\|_{\infty} < \epsilon $$

而对于有目标的FGSM，我们的想法则是：

$$ \operatorname{minimize }J(\theta,x^{\prime},y^{\prime}),\quad\text{s.t.}\|x^{\prime}-x\|_{\infty} < \epsilon $$

其中，$x$ 为原始图像，$x^{\prime}$ 为对抗攻击后的图像，$y$ 为真实的标签，$y^{\prime}$ 为对抗攻击中的目标标签。

所以它的实现公式为：

$$ x^{\prime}=x{\color{red}-}\epsilon\cdot\mathrm{sign}(\nabla_{x}J(\theta,x,y^{{\color{red}\prime}})) $$

此处与FGSM相比只有微小的区别。

源代码

源代码见Github-EPTansuo. FGSM-learn

参考：

https://pytorch.org/tutorials/beginner/blitz/cifar10_tutorial.html

https://colab.research.google.com/github/ashishpatel26/Awesome-Pytorch-Tutorials/blob/main/17.Pytorch Transfer learning with Caltech101.ipynb

https://github.com/Harry24k/FGSM-pytorch

https://github.com/1Konny/FGSM